标量，向量，矩阵和张量

标量（scalar）：一个标量就是一个单独的数。用斜体表示标量，如 $s∈R$ .

向量（vector）：一个向量是一列数，我们用粗体的小写名称表示向量。比如 $x$ ，将向量x 写成方括号包含的纵柱：

${\bf x}= \begin {bmatrix} x_1\\x_2\\ \vdots \\x_n\\ \end{bmatrix}$

矩阵（matrix）：矩阵是二维数组，我们通常赋予矩阵粗体大写变量名称，比如 $A$ 。如果一个矩阵高度是 $m$ ，宽度是 $n$ ，那么说 $\bf A\in \bf R ^{m \times n}$ 。一个矩阵可以表示如下：

${\bf A}= \begin{bmatrix} x_{11} &x_{12}\\ x_{21} & x_{22}\\ \end{bmatrix}$

张量（tensor）：某些情况下，我们会讨论不止维坐标的数组。如果一组数组中的元素分布在若干维坐标的规则网络中，就将其称为张量。用 $A$ 表示，如张量中坐标为 $(i,j,k)$ 的元素记作 $A_{i,j,k}$ 。
转置（transpose）：矩阵的转置是以对角线为轴的镜像，这条从左上角到右下角的对角线称为主对角线（main diagonal）。将矩阵 $A$ 的转置表示为 $A^⊤$ 。定义如下：

$({\bf A^\top})_{i,j}=\bf A_{j,i}$

${\bf A} = \begin{bmatrix} x_{11} &x_{12}\\ x_{21} & x_{22}\\ x_{31} & x_{32} \end{bmatrix} \implies {\bf A^\top}= \begin{bmatrix} x_{11} &x_{21}&x_{31} \\ x_{21} & x_{22}& x_{32} \end{bmatrix}$

向量运算

加法

设 $\overrightarrow{v}=\begin{bmatrix} 1 \\ 2 \end{bmatrix}$ ， $\overrightarrow{w}=\begin{bmatrix}3\\ -1\end{bmatrix}$ 则 $\overrightarrow{v}+\overrightarrow{w}=\begin{bmatrix}4\\ 1\end{bmatrix}$

数乘

设 $\overrightarrow{v}=\begin{bmatrix} 3 \\ 1 \end{bmatrix}$ ，则 $2\overrightarrow{v}=\begin{bmatrix} 3\times 2 \\ 1\times 2 \end{bmatrix}=\begin{bmatrix} 6 \\ 2 \end{bmatrix}$

矩阵-向量的乘积

矩阵是空间的线性变换，矩阵与向量相乘便是将向量进行线性变换的结果。

$A\overrightarrow{v}=\begin{bmatrix} \overset{i}{1} & \overset{j}{3}\\ -2 & 0 \end{bmatrix}\begin{bmatrix} -1\\ 2 \end{bmatrix}=\begin{bmatrix} -1\times 1+2\times 3\\ -1\times -2+2\times 0 \end{bmatrix}=\begin{bmatrix} 5\\ 2 \end{bmatrix}$

向量-向量的乘积

向量可以看成一个矩阵，这个矩阵将空间压缩到了一维空间。

$\overrightarrow{w}\cdot \overrightarrow{v}=|\overrightarrow{w}|| \overrightarrow{v}|cos\theta =\begin{bmatrix} 1\\ -2 \end{bmatrix}\cdot\begin{bmatrix} 4\\ 3 \end{bmatrix}=4\times 1+3\times (-2)=-2$ 向量

$\overrightarrow{v}$ 在向量

$\overrightarrow{w}$ 上的投影乘以向量

$\overrightarrow{w}$ 的长度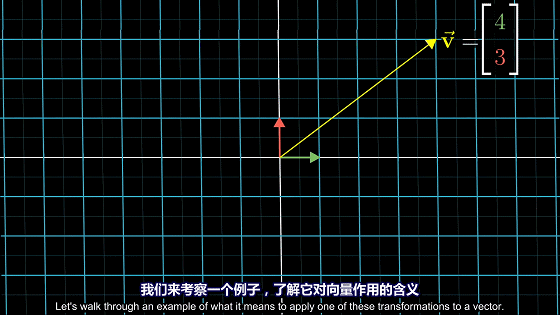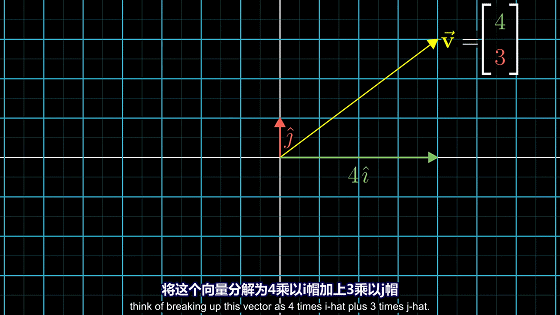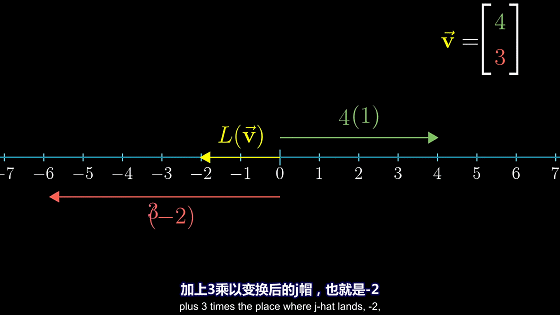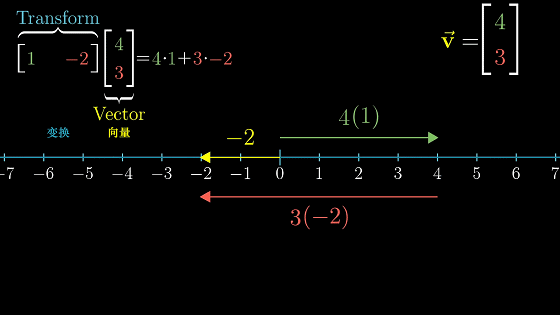

向量的叉积

向量的叉积是一个向量，向量 $\overrightarrow{p}$ 的方向垂直于 $\overrightarrow{w}$ 与 $\overrightarrow{v}$ 的平面，向量 $\overrightarrow{p}$ 的模是 $\overrightarrow{w}$ 与 $\overrightarrow{v}$ 所围成平面的面积(行列式)。

$\overrightarrow{w}\times \overrightarrow{v}=|\overrightarrow{w}|| \overrightarrow{v}|sin\theta =\overrightarrow{p}$

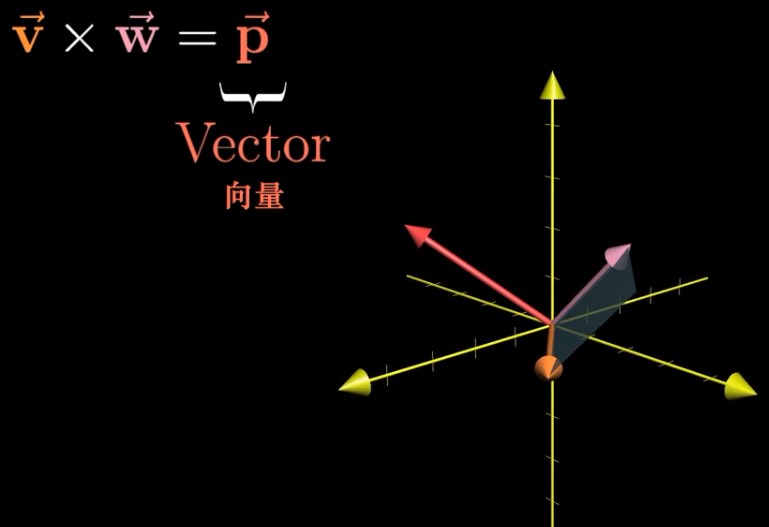
高维情况

$\overrightarrow{w}\times \overrightarrow{v}=\overrightarrow{p}$ 则

$\begin{align*} p_1 &=v_2\cdot w_3-v_3\cdot w_2 \\ p_2 &=v_3\cdot w_1-v_1\cdot w_3 \\ p_3 &=v_1\cdot w_2-v_2\cdot w_1 \end{align*}$

矩阵的运算

对向量的线性空间变换

矩阵加减法

对应位置的元素相加相减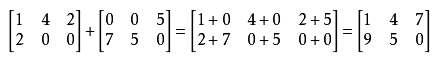

矩阵数乘

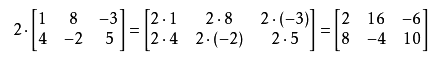
矩阵转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵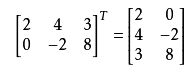

矩阵共轭

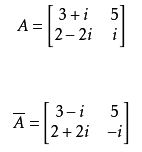
矩阵共轭转置

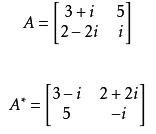
矩阵-向量的乘积

矩阵是空间的线性变换，矩阵与向量相乘便是将向量进行线性变换的结果。

矩阵-矩阵的乘积

矩阵是一种线性变换，矩阵与矩阵相乘便是将空间进行线性变换之后再次进行线性变换。矩阵与矩阵的乘积是一种对于空间的复合线性变换。变换吸纳从右侧开始一次向左侧进行变换。线性变换的过程如下图所示：

矩阵-矩阵的计算过程如下所示 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & -2\\ 1 & 0 \end{bmatrix}=\left\{\begin{matrix}1\times \begin{bmatrix}0\\ 1\end{bmatrix}+1\times \begin{bmatrix}2\\ 0\end{bmatrix} \\-2\times \begin{bmatrix}0\\ 1\end{bmatrix}+0\times \begin{bmatrix}2\\ 0\end{bmatrix}\end{matrix}\right.=\begin{bmatrix} 2 &0 \\ 1 & -2 \end{bmatrix}$
计算过程去下图所示

矩阵-矩阵乘积的性质

结合律即 $(AB)C = A(BC)$
分配率即 $A(B + C) = AB + AC$
注意哦，矩阵乘法没有交换律，即 $AB ≠BA$

矩阵的逆

矩阵 $A ∈ R^{n×n}$ 的逆,写作 $A^{−1}$ ，是一个矩阵，并且是唯一的。是对矩阵 $A$ 空间操作的逆变换。同时 $AA^{−1}$ 也可以理解为矩阵 $A$ 除以矩阵 $A$ 等于单位矩阵 $I$ ， $A^{−1}A = I = AA^{−1}.$

注意不是所有的矩阵都有逆。例如非方阵，是没有逆的。然而，即便对于一些方阵，它仍有可能不存在逆。如果 $A^{−1}$ 存在，我们称矩阵 $A$ 是可逆的或非奇异的，如果不存在，则称矩阵 $A$ 不可逆或奇异。如果一个方阵 $A$ 有逆 $A^{−1}$ ，它必须满秩

矩阵的秩

矩阵的秩实际上的经过矩阵操作后空间的维数。在矩阵A中，非零子式的最高阶数称为矩阵A的秩，记为或秩。规定零矩阵的秩为零。

求解思路

$矩阵A\xrightarrow{初等行变换}阶梯形矩阵B。$ 则 $r(A)=r(B)=$ ( $B$ 中非零行的行数)

例子
-
求矩阵 $A=\begin{bmatrix} 2 &-3 &8 & 2\\ 2 &12 &-2 & 12\\ 1 &3 & 1 & 4 \end{bmatrix}$ 的秩。

解：

$A= \begin{bmatrix} 2 &-3 &8 & 2\\ 2 &12 &-2 & 12\\ 1 &3 & 1 & 4 \end{bmatrix}\rightarrow \begin{bmatrix} 1 &3 &1 & 4\\ 2 &-3 &8 & 2\\ 2 &12 &-2 & 12 \end{bmatrix}\rightarrow \begin{bmatrix} 1 &3 &1 & 4\\ 0 &-9 &6 & -6\\ 0 &6 &-6 & 4 \end{bmatrix}\rightarrow \begin{bmatrix} 1 &3 &1 & 4\\ 0 &3 &-2 &2\\ 0 &0 &-0 & 0 \end{bmatrix}$

因此 $r(A)=2$

矩阵的迹

方阵 $A ∈ R^{n×n}$ 的迹，记作 $tr(A)$ ，或可以省略括号表示成 $trA$ ，是矩阵的对角线元素之和: $trA=\sum_{i=1}^{n}A_{ii}$

性质
1. 对于 $A ∈ R^{n×n}， trA = trA^T .$
2. 对于 $A，B ∈ R^{n×n}， tr(A + B) = trA + trB.$
3. 对于 $A ∈ R^{n×n}， t ∈ R， tr(t\ast A) = t\ast trA.$
  1.对于方阵 $A,B,C，trABC = trBCA = trCAB$ ，即使有更多的矩阵相乘，这个性质也不变.

正交矩阵

如果 $x^Ty = 0$ ，则两个向量 $x，y ∈ R^n$ 是正交的。对于一个向量 $x ∈ R^n$ ，如果 $|x|=1$ 则是 $x$ 归一化的。对于一个方阵 $U ∈ R^{n×n}$ ，如果所有列都是彼此正交和归一化的，（列就称为标准正交）则这个方阵是正交的（注意在讨论向量或矩阵时，正交具有不同的含义）。根据正交和归一化的定义可得：

$U^T U = I = UU^T$ 一个正交矩阵的逆矩阵的是它转置,正交矩阵必须是方阵