特征值与特征向量

定义

特征向量

矩阵在空间变换过程中，没有发生旋转的向量。因此特征向量可以看过空间变换的旋转轴。

特征值

特征向量在变换中拉伸或压缩比例的因子

计算

$\vec{v}$为特征向量，$\lambda$为特征值。求解如下所示：

$$\begin{align*} A\vec{v}&=\lambda \vec{v} \\ A\vec{v}- \lambda \vec{v} &= \vec{0}\\ (A- \lambda I)\vec{v} &= \vec{0} \end{align*}$$

存在一个非零向量 $\vec{v}$ 使得 $(A- \lambda I)\vec{v} = \vec{0}$ 则

$$det(A- \lambda I)=0$$

求出$\lambda$即特征值，带入特征值$\lambda$解得特征向量$\vec{v}$。

对角矩阵

对角矩阵的所有基向量都是特征向量

$$\begin{bmatrix} -5 & 0 & 0 & 0\\ 0 & -2 & 0 & 0\\ 0 & 0 & -4 & 0\\ 0 & 0 & 0 & 4 \end{bmatrix}$$

对角矩阵的优势

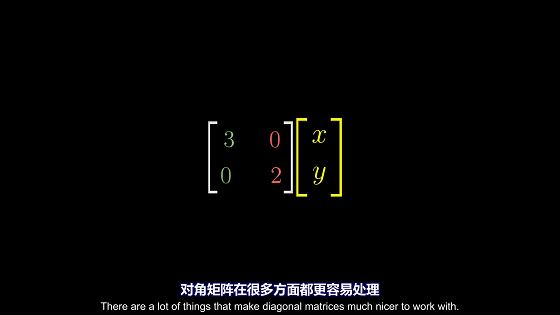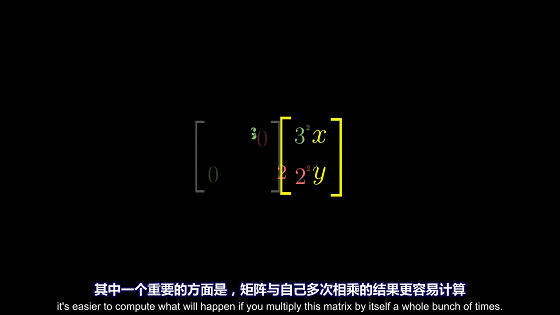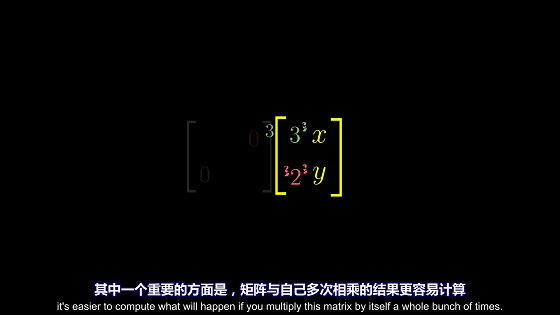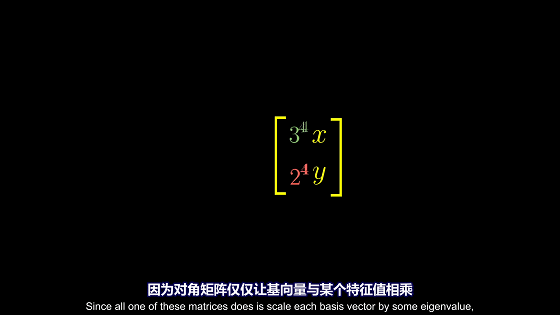
对角矩阵的使用

求出特征向量，利用基变换将原空间变换为以特征向量为基的空间，再利用基变换将以特征向量为基的空间变换为原空间