真实类别	预测为正例	预测为反例
正例	TP(真正例)	FN(假反例)
反例	FP(假正例)	TN(真反例)

# 混淆矩阵
from sklearn.metrics import confusion_matrix

confusion = confusion_matrix(y_test,y_prob)

准确率、错误率、召回率、查准率

名称	公式	说明
准确率（$Accuracy$）	$\frac{TP+TN}{TP+TN+FP+FN}$	预测正确的比例
错误率（$Error$）	$\frac{FP+FN}{TP+TN+FP+FN}$	预测错误的比例
召回率/查全率（$Recall$）	$\frac {TP}{TP+FN}$	真正例被预测正确的比例。有多少好瓜被选出来
精确率/查准率（$Precision$）	$\frac{TP}{TP+FP}$	预测为正例中正确的比例。预测为的好瓜的类别中有多少好瓜

1
2
3

'''准确率、召回率、f分数'''
from sklearn.metrics import classification_report
print(classification_report(y_test,y_prob,target_names=['not nine','nine']))

P-R曲线与平衡点

一般来说，查准率高的时候，召回率偏低；召回率高的时候，查准率往往降低。以西瓜问题为例：查准率指的是所有预测为好瓜的西瓜中，真正的好瓜所占的比例；召回率指的是真正的好瓜中，有多少好瓜被挑出来了。如果所有西瓜都预测为好瓜则召回率为1，但是查准率就会降低因为所有坏瓜也预测为了好瓜。

'''准确率与召回率曲线'''
from sklearn.metrics import precision_recall_curve
#y_prob[:,1]是一个2维数组，1表示第1个类别
precision,recall,threshold=precision_recall_curve(y_test,y_prob[:,1])   

import numpy as np
import matplotlib.pyplot as plt
close_zero = np.argmin(np.abs(threshold))  # 找到最接近0的阈值
plt.plot(recall[close_zero],precision[close_zero],'o',markersize=10,label='threshold zero',fillstyle = 'none',c = 'k',mew = 2)
plt.plot(recall,precision,label='precision recall curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()

P-R曲线

以查准率P为纵轴，召回率R为横轴作图，就得到了查准率-召回率曲线，称为“P-R曲线”。。对于一个排序模型来说，其P-R曲线上的一个点代表着，在某一阈值下，模型将大于该阈值的结果判定为正样本，小于该阈值的结果判定为负样本，此时返回结果对应的召回率和精确率。 整条P-R 曲线是通过将阈值从高到低移动而生成的，左边的阈值较高，右边的阈值较低。

1565235635992

$y轴-查准率（精确率）P = \frac {TP} {TP+FP} \\ x轴-查全率（召回率）R = \frac {TP} {TP+FN}$

在比较两个模型的性能时，如果一个学习器的P-R曲线被另外一个学习器P-R曲线包住，那么后者的性能优于前者（此时后者的查全率跟查准率都高于前者），如上图，A的性能优于C，B的性能也优于C；如果两个学习器的曲线有交叉点（如A和B），那么难以断定两个学习器性能的优劣，只能在具体的查准率或者查全率条件下进行比较。

举例计算

假设有4个样本，样本的标签分别为 $0,1,0,1$；模型的预测概率分别为$0.1,0.35,0.4,0.8$；

label	0	1	0	1
pred	0.1	0.35	0.4	0.8
阈值	0.1	0.35	0.4	0.8

那么在阈值分别取$0.1, 0.35, 0.4, 0.8$的时候。分别判断出每个pred是TP/FP/TN/FP中的哪个，进而得出当前阈值下的R和P，也就是(Recall, Precision)这一P-R曲线图上的点；对于所有阈值都计算相应的(Recall, Precision),则得到完整的ROC曲线上的几个关键点。

阈值	样本1	样本2	样本3	样本4	$precision=\frac{TP}{TP+FP}$	$recall=\frac {TP}{TP+FN}$
0.1	FP	TP	FP	TP	0.5	$\frac{2}{2+0}=1$
0.35	TN	TP	FP	TP	$\frac{2}{3}$	$\frac{2}{2+0}= 1 $
0.4	TN	FN	FP	TP	0.5	$\frac{1}{1+1}=0.5$
0.8	TN	FN	TN	TP	1	$\frac {1} {1+1}=0.5$

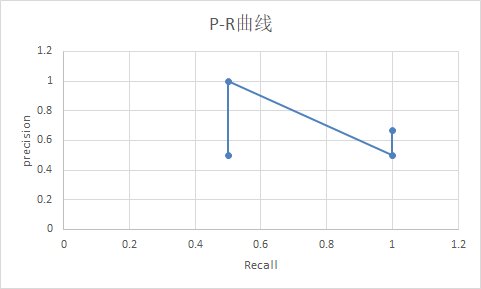
平衡点（BEP-》Break-Even Point）

如果两个学习器的P-R曲线有交叉点（如A和B），那么通过平衡点或者F1度量断定两个学习器性能的优劣
平衡点(Break-Even Point，简称BEP)指得是“P=R”时候的取值，如上图，C的的BEP是0.64,。基于BEP的比较，可以认为学习器A优于B。

F1指数与$F_\beta$指数

正如上文所述，Precision和Recall指标有时是此消彼长的，即精准率高了，召回率就下降，在一些场景下要兼顾精准率和召回率，最常见的方法就是F1指数与$F_\beta$指数。

F1指数

F1指数实际为查准率和召回率的调和平均数。例如小明跑步10公里，前面5公里用了1小时，后面5公里用了2小时，其平均速度为$\frac{10}{v}=(\frac {5}{1}+ \frac {5}{2})$

$\frac 1 {F1} =\frac 1 2 (\frac 1{P}+\frac 1 R)$

$F_\beta$指数

对于特定的应用场景，查准率和查全率的重视度是不一样的。例如在追捕逃犯时，希望尽可能的不遗漏逃犯，因此查全率较为重要；而在搜索引擎的搜索过程中，希望给用户精准的搜索信息，因此查准率更为重要。F1度量的更一般形式——$F_β$，修改了路程

$\frac{1}{F_\beta }=\frac{1}{1+\beta ^2}(\frac{1}{P}+\frac{\beta ^2}{R})\\$

$β=R/P$ ，其中$β$值越大召回率越重要，$β$值越小查准率越重要。$β$值为两者重要性的比例

G-mean指数

G-mean是正例的召回率与负例的召回率的综合指标。与F1的比较：在数据平衡度不是很大的情况下，F1和G-mean可以作为较好的评测指标，但是当训练样本很不平衡时，G-mean更好。

$G - mean = \sqrt{\frac {TP}{TP+FN}\times \frac {TN}{TN+FP}} = \sqrt {查全率（召回率）真正例 \times 查全率（召回率）真负例}$

ROC曲线与AUC

'''ROC与AUC'''
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
fpr,tpr,thresholds = roc_curve(y_test ,y_prob[:,1] )
plt.plot(fpr,tpr,label = 'ROC Curve')
plt.xlabel('FPR')
plt.ylabel('TPR(recall)')

# ROC曲线
import numpy as np
close_zero = np.argmin(np.abs(thresholds))  # 0的位置
plt.plot(fpr[close_zero],tpr[close_zero],'o',markersize = 10,label = 'threshold zero',fillstyle = 'none',c = 'k' ,mew = 2)
plt.legend(loc = 4)

# AUC
from sklearn.metrics import roc_auc_score
ruc_auc = roc_auc_score(y_test ,y_prob[:,1])

ROC曲线

真正例率指的是真实正例中有多少被预测为正例，假正例率指的是真实反例中有多少被预测为正例。可以看出TPR和Recall的形式是一样的，就是查全率了，FPR就是1-负例的召回率。如果所有西瓜都预测为好瓜则查全率为1，但是假正例率也会升高因为所有坏瓜也预测为了好瓜。

$y轴-真正例率 TPR = \frac {TP}{TP+FN}=正例的召回率=\frac{预测为正且的正样本数}{实际为正的样本数}\\ x轴-假正例率 FPR = \frac {FP}{TN+FP}=1-\frac{TN}{TN+FP}=1-负例的召回率=\frac{预测为正的负样本数}{实际的负样本数}$

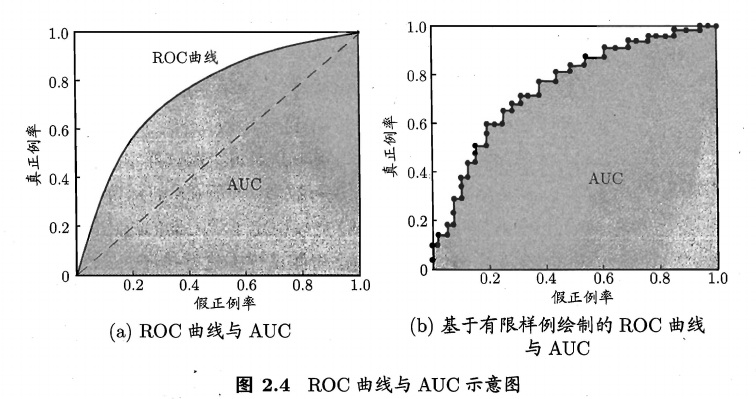
1565246937404

以真正例率$TPR $为纵轴，假正例率$FPR$为横轴作图，就得到了“ROC曲线”。。对于一个排序模型来说，其ROC曲线上的一个点代表着，在某一阈值下，模型将大于该阈值的结果判定为正样本，小于该阈值的结果判定为负样本，此时返回结果对应的真正例率和假正例率。 整条ROC曲线是通过将阈值从高到低移动而生成的，左边的阈值较高，右边的阈值较低。

举例计算

假设有4个样本，样本的标签分别为 $0,1,0,1$；模型的预测概率分别为$0.1,0.35,0.4,0.8$；

label	0	1	0	1
pred	0.1	0.35	0.4	0.8
阈值	0.1	0.35	0.4	0.8

那么在阈值分别取$0.1, 0.35, 0.4, 0.8$的时候。分别判断出每个pred是TP/FP/TN/FP中的哪个，进而得出当前阈值下的TPR和FPR，也就是(FPR, TPR)这一ROC曲线图上的点；对于所有阈值都计算相应的(FPR, TPR),则得到完整的ROC曲线上的几个关键点。

阈值	样本1	样本2	样本3	样本4	$TPR=\frac {TP}{TP+FN}$	$FPR\frac {FP}{TN+FP}$
0.1	FP	TP	FP	TP	$\frac{2}{2+0}=1$	$\frac{2}{0+2}=1$
0.35	TN	TP	FP	TP	$\frac{2}{2+0}= 1 $	$\frac{1}{1+1}=0.5$
0.4	TN	FN	FP	TP	$\frac{1}{1+1}=0.5$	$\frac{1}{1+1}=0.5 $
0.8	TN	FN	TN	TP	$\frac {1} {1+1}=0.5$	0

1565855471447

AUC指数

AUC：ROC曲线的线下面积。与P-R曲线类似，如果学习器A的ROC曲线被学习器B完全“包住”，那么后者性能优于前者（相同的假正例率，其真正例率更高）。但是当两个曲线有交点时，则需要比较曲线下的面积AUC(Area Under ROC Curve)。

k-s指标

K-S(Kolmogorov-Smirnov)统计量越大，表示模型能够将正、负客户区分开的程度越大。KS值的取值范围是[0，1] 。与ROC曲线相似

'''ks'''
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
fpr,tpr,thresholds = roc_curve(y_test ,y_prob[:,1])   #计算fpr与tpr
thresholds=np.flipud(thresholds)         #thresholds逆序
plt.plot(thresholds,fpr,label = 'fpr')
plt.plot(thresholds,tpr,label = 'tpr')
plt.plot(thresholds,tpr-fpr,label = 'ks')
plt.xlabel('threshold')
plt.ylabel('Gradual ratio')   #累计占比
plt.xlim((0,1))
plt.show()
ks=max(tpr-fpr)

ks曲线

$TPR = TP/(TP+FN)=正例的召回率=\frac{预测为正且的正样本数}{实际为正的样本数} \\ FPR = FP/(FP+TN)=1-\frac{TN}{TN+FP}=1-负例的召回率=\frac{预测为正的负样本数}{实际的负样本数}$

洛伦兹线：两条线，其横轴是模型评分的阈值，纵轴是$TPR$（真正类率）与$FPR$（假正类率）的值

K-S曲线：洛伦兹线中两条线的差值（$TPR-FPR$），值范围[0，1] 。

我们用一个风控模型预测一个人是好人的概率，图中黑线的洛伦兹线（$TPR$与$FPR$）、红线的ks曲线。横坐标是模型评分的阈值，当阈值为0时，所有的用户被预测为坏用户，$TPR=FPR=0$；当阈值为1时，所有用户被预测为好用户，$TPR=FPR=1$。

这两条曲线之间的差值（$TPR-FPR$），就是K-S曲线。如图所示，给定一个通过率20%（拒绝率80%），则该模型可以挑出来60%的好人，同时漏进来8%的坏人（92%的坏人都被拒绝掉了）。那么K-S曲线在这个通过率上的值，就是60%-8%=0.52。

K-S统计量

K-S曲线中的最大值被称为K-S统计量。其取值在0到1之间。如果是随机抽样，好人的洛伦兹曲线跟坏人的是重合的，K-S统计量为0。而最理想的风控模型，好人和坏人完全分开，K-S统计量的值为1。

多类别评估

1
2
3

'''准确率、召回率、f分数'''
from sklearn.metrics import classification_report
print(classification_report(y_test,y_prob)

              precision    recall  f1-score   support

           0       1.00      0.67      0.80    187169             #类别0的评估
           1       0.01      0.66      0.02      1144             #类别1的评估

   micro avg       0.67      0.67      0.67    188313             #micro平均值
   macro avg       0.50      0.67      0.41    188313             #macro平均值
weighted avg       0.99      0.67      0.80    188313             #weighted平均值

举例计算

Label	1	2	3	2	3	3	1	2	2
Prediction	2	2	1	2	1	3	2	3	2

micro avg

TP：分类正确的样本。如绿色所示
FN=FP：分类错误的样本。如红色所示

$precision \;\;\; P=\frac{TP}{TP+FP}=\frac{4}{4+5}=0.4444\\ recall\;\;\;\;R=\frac{TP}{TP+FN}=\frac{4}{4+5}=0.4444\\ F1=2\times \frac{\frac{4}{9} \times \frac{4}{9}}{\frac{4}{9} + \frac{4}{9}}=0.44444$

macro avg

	TP	FP	FN	precision	recall	F1
class 1	0	2	2	0	0	0
class 2	3	2	1	$\frac{3}{5}=0.6$	$\frac{3}{4}=0.75$	$\frac{2}{3}$
class 3	1	1	2	$\frac{1}{2}$	$\frac{1}{3}$	$\frac{2}{5}$

precision：$(0+\frac{3}{5}+\frac{1}{2})/3=0.36667$
recall：$(0+\frac{3}{4}+\frac{1}{3})/3=0.3611111$
F1：$(0+\frac{2}{3}+\frac{2}{5})/3=0.3555556$

weighted avg

加入类别的权重。3类样本的权重分别如下所示

class1	class2	class3
2/9	4/9	3/9

precision：$\frac{2}{9} \times 0+\frac{4}{9} \times \frac{3}{5}+ \frac{3}{9} \times \frac{1}{2}=0.4333333$
recall：$\frac{2}{9} \times 0+\frac{4}{9} \times \frac{3}{4}+ \frac{3}{9} \times \frac{1}{3}=0.444444444$
F1：$\frac{2}{9} \times 0+\frac{4}{9} \times \frac{2}{3}+ \frac{3}{9} \times \frac{2}{5}=0.429630$

综合说明


micro avg	受不平衡样本影响较小。precision=recall=f1-score
macro avg	受不平衡样本影响较小。几个类别的平均数
weighted avg	受不平衡样本影响较大。倾向于较大的类别

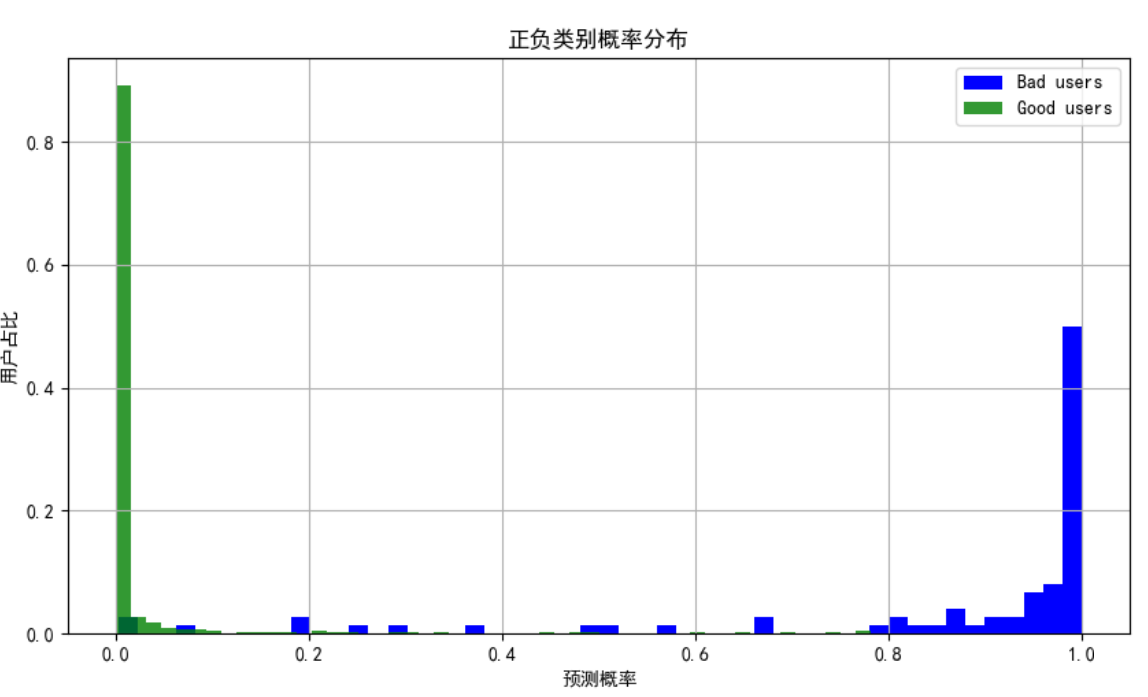
不同类别的概率分布图

判断模型的分类性能，分的开不开。

def class_porb(true_label,guess_label)
    """
        用户正负比例的概率分布图
    Args:
        true_label: 测试样本真实标签序列
        guess_label: 测试样本预测标签序列
    returns:
        None
    """
    plt.hist(guess_label[true_label == 1], bins=50, color='blue',
             weights=np.ones_like(guess_label[true_label == 1]) / len(guess_label[true_label == 1]), label='Bad users')
    plt.hist(guess_label[true_label == 0], bins=50, color='green', alpha=0.8,
             weights=np.ones_like(guess_label[true_label == 0]) / len(guess_label[true_label == 0]), label='Good users')
    plt.grid()
    plt.xlabel(u'预测概率')
    plt.ylabel(u'用户占比')
    plt.title(u'正负类别概率分布')
    plt.legend(loc='best')
    plt.show()

回归评估指标

均方误差（Mean Squared Error，MSE） $MSE=\frac{1}{m} \sum_{i=1}^{m}(f_i-y_i)^2$

均方根误差（Root Mean Squard Error，RMSE）
$RMSE=\sqrt{\frac{1}{m} \sum_{i=1}^{m}(f_i-y_i)^2}$
它的意义在于开个根号后，误差的结果就与数据是一个级别的，可以更好地来描述数据。标准误差对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。
平均绝对误差（Mean Absolute Error，MAE）
$MAE=\frac{1}{m}\sum_{i=1}^{m}|f_i-y_i|$
R-squared
$R^2=1-\frac{\sum_{i=1}^m(f_i-y_i)^2}{\sum_{i=1}^m(\bar y_i-y_i)^2}=1-\frac{\frac{1}{m}\sum_{i=1}^m(f_i-y_i)^2}{\frac{1}{m}\sum_{i=1}^m(\bar y_i-y_i)^2}=1-\frac{MSE(f,y)}{Var(y)}$

总结

下面的简单总结，主要是对比各个参数，并说明不平衡数据集对参数的影响。

真实类别	预测为正例	预测为反例
正例	TP(真正例)	FN(假反例)
反例	FP(假正例)	TN(真反例)

名称	公式	说明	测试集为不平衡数据集
准确率（$Accuracy$）	$\frac{TP+TN}{TP+TN+FP+FN}$	预测正确的比例	影响较大，因为包含两个不平衡样本的数据
错误率（$Error$）	$\frac{FP+FN}{TP+TN+FP+FN}$	预测错误的比例	影响较大，因为包含两个不平衡样本的数据
召回率/查全率（$Recall$）	$\frac {TP}{TP+FN}$	实际为正样本中有多少被预测出来	无影响，$TP、FN$全部来自实际正例数据集
精确率/查准率（$Precision$）	$\frac{TP}{TP+FP}$	预测为正样本中有多少是真实的正样本	影响较大，因为包含两个不平衡样本的数据
PR曲线	横坐标为recall 纵坐标为precision	左侧的阈值大，右侧的阈值小	影响较大，因为纵坐标包含两个不平衡样本的数据
F1指数	$\frac{1}{F1}=\frac{1}{P}+\frac{1}{R}$	因为recall与precision存在对立关系，为了综合评估recall与precision。所以提出F1指数	影响较大，因为precision包含两个不平衡样本的数据
$F_\beta$指数	$\frac{1}{F_\beta }=\frac{1}{1+\beta ^2}(\frac{1}{P}+\frac{\beta ^2}{R})$	通过调整$\beta$的比例，调整$F_\beta$的侧重关系	影响较大，因为precision包含两个不平衡样本的数据
G-mean	$\sqrt{\frac {TP}{TP+FN}\times \frac {TN}{TN+FP}} $	$\sqrt {（召回率）正例 \times （召回率）负例}$ 越高越好；为了解决样本不平衡问题	无影响，因为召回率没有使用不平衡数据相比
ROC曲线	横坐标为，$\frac {FP}{TN+FP}=1-负例的召回率$ 纵坐标为，$\frac {TP}{TP+FN}=正例的召回率$	左侧的阈值大，右侧的阈值小	无影响，因为召回率没有使用不平衡数据相比
AUC	ROC的面积	越大越好	无影响，因为召回率没有使用不平衡数据相比
KS	横坐标阈值纵坐标为正例的召回率以及（1-负例的召回率）之间的差值	目的选定阈值，使得正例的召回率与1-负例的召回率差值最大。与ROC曲线具有一定的相似性	无影响，因为召回率没有使用不平衡数据相比